All Together Now! We can have all of them in one equation: y = A sin (B (x + C)) + D amplitude is A period is 2π/B phase shift is C (positive is to the left) vertical shift is D And here is how it looks on a graph: Note that we are using radians here, not degrees, and there are 2 π radians in a full rotation. Example: sin (x)
Period of sinusoidal functions from graph – YouTube
Nov 27, 2023Identify the amplitude, vertical shift, period and frequency of the following function. Then graph the function. f(x) = 2sin(x 3) + 1. a = 2, b = 1 3, d = 1. The amplitude is 2, the vertical shift is 1, and the frequency is 1 3. The period would be 2π 1 3, or 6π. Often the most challenging part of graphing periodic functions is labeling the

Source Image: k12.libretexts.org
Download Image
This video continues with finding the period of a sinusoidal function from its equation by looking at several more example problems from the Khan Academy exe
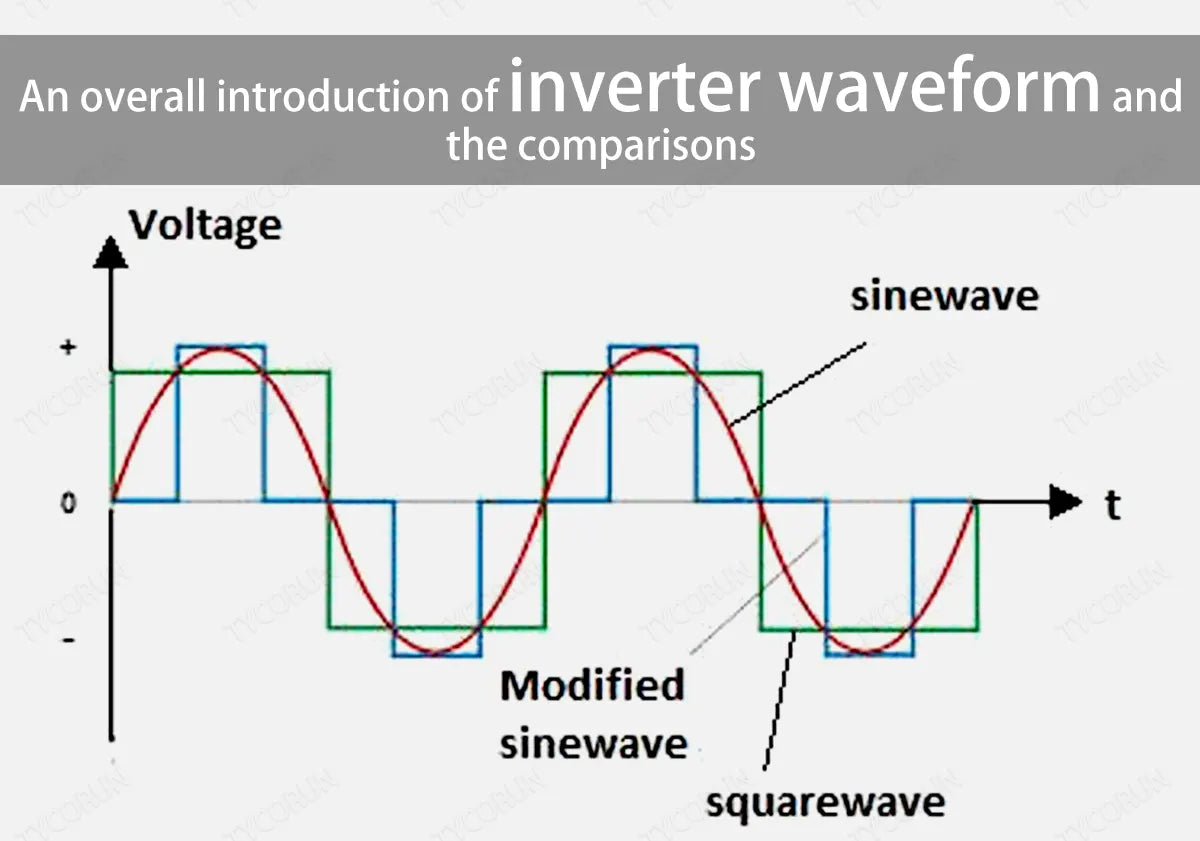
Source Image: tycorun.com
Download Image
Period of Sinusoidal Functions from Equation (1 of 2) – YouTube Nov 21, 2023The sine function is the function eqf(x) = sin(x) /eq, and is one of the most basic functions used in the study of trigonometry. The sine function is cyclic, meaning that it repeats itself
Source Image: bartleby.com
Download Image
What Is The Period Of The Sinusoidal Function
Nov 21, 2023The sine function is the function eqf(x) = sin(x) /eq, and is one of the most basic functions used in the study of trigonometry. The sine function is cyclic, meaning that it repeats itself Nov 21, 2023A sinusoidal function is a function that is based on the sine function, which is a periodic function that smoothly oscillates between high and low values. Sinusoidal functions can
Sinusoidal Functions | bartleby
Finding features from graph Given the graph of a sinusoidal function, we can analyze it to find the midline, amplitude, and period. Consider, for example, the following graph. It has a maximum point at ( 1, 7) , then a minimum point at ( 3, 3) , then another maximum point at ( 5, 7) . Graph sinusoidal functions by plotting points – YouTube

Source Image: youtube.com
Download Image
Sinusoidal Functions with Different Time Periods – YouTube Finding features from graph Given the graph of a sinusoidal function, we can analyze it to find the midline, amplitude, and period. Consider, for example, the following graph. It has a maximum point at ( 1, 7) , then a minimum point at ( 3, 3) , then another maximum point at ( 5, 7) .

Source Image: m.youtube.com
Download Image
Period of sinusoidal functions from graph – YouTube All Together Now! We can have all of them in one equation: y = A sin (B (x + C)) + D amplitude is A period is 2π/B phase shift is C (positive is to the left) vertical shift is D And here is how it looks on a graph: Note that we are using radians here, not degrees, and there are 2 π radians in a full rotation. Example: sin (x)
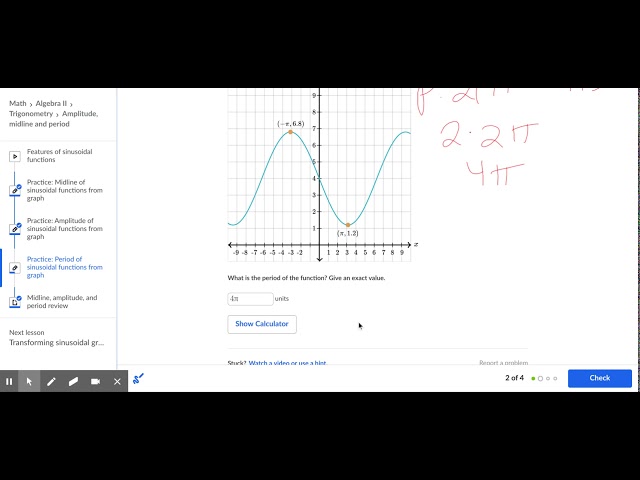
Source Image: m.youtube.com
Download Image
Period of Sinusoidal Functions from Equation (1 of 2) – YouTube This video continues with finding the period of a sinusoidal function from its equation by looking at several more example problems from the Khan Academy exe

Source Image: youtube.com
Download Image
Amplitude, Period, Phase Shift and Frequency Feb 13, 2022Period and Frequency of Sinusoidal Functions. The general equation for a sinusoidal function is: f (x)=±a⋅sin (b (x+c))+d. The ± ± controls the reflection across the x x -axis. The coefficient a a controls the amplitude. The constant d d controls the vertical shift. Here you will see that the coefficient b b controls the horizontal stretch.

Source Image: mathsisfun.com
Download Image
Period of Sinusoidal Functions from Equation: Formula for the Period – YouTube Nov 21, 2023The sine function is the function eqf(x) = sin(x) /eq, and is one of the most basic functions used in the study of trigonometry. The sine function is cyclic, meaning that it repeats itself
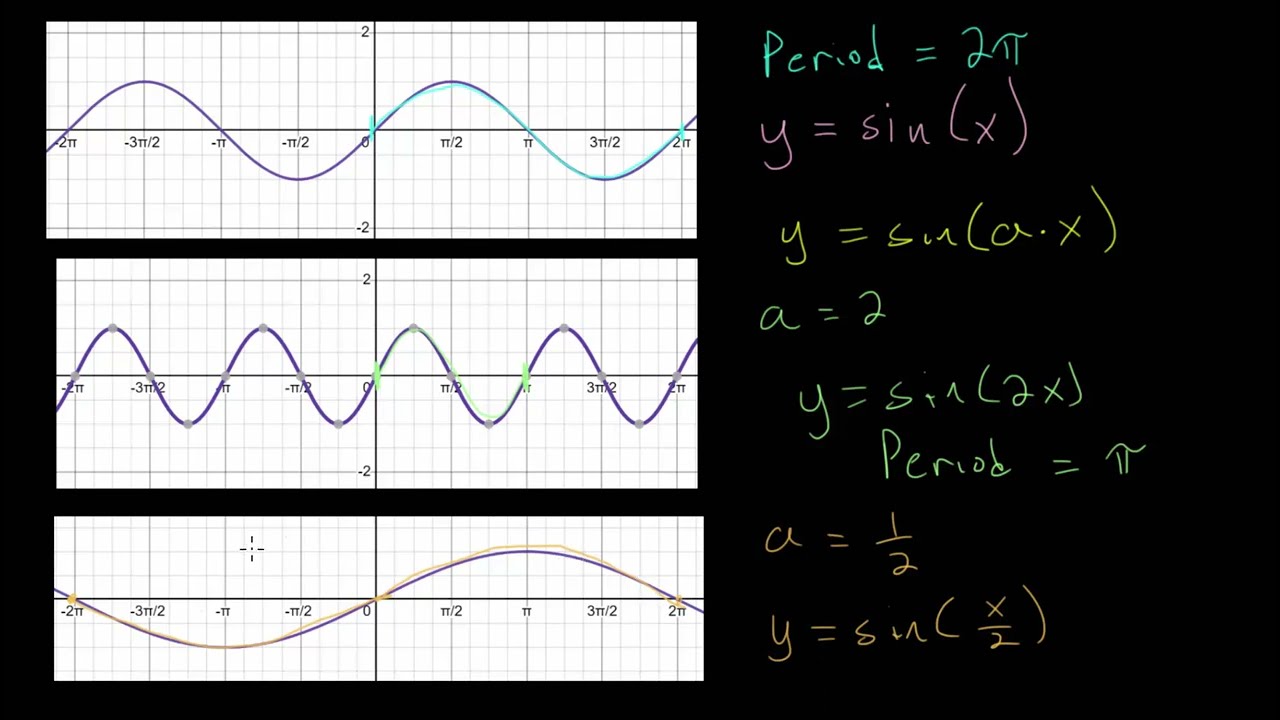
Source Image: youtube.com
Download Image
Sinusoidal Functions with Different Time Periods – YouTube Nov 21, 2023A sinusoidal function is a function that is based on the sine function, which is a periodic function that smoothly oscillates between high and low values. Sinusoidal functions can

Source Image: m.youtube.com
Download Image
Sinusoidal Functions with Different Time Periods – YouTube
Sinusoidal Functions with Different Time Periods – YouTube Nov 27, 2023Identify the amplitude, vertical shift, period and frequency of the following function. Then graph the function. f(x) = 2sin(x 3) + 1. a = 2, b = 1 3, d = 1. The amplitude is 2, the vertical shift is 1, and the frequency is 1 3. The period would be 2π 1 3, or 6π. Often the most challenging part of graphing periodic functions is labeling the
Period of Sinusoidal Functions from Equation (1 of 2) – YouTube Period of Sinusoidal Functions from Equation: Formula for the Period – YouTube Feb 13, 2022Period and Frequency of Sinusoidal Functions. The general equation for a sinusoidal function is: f (x)=±a⋅sin (b (x+c))+d. The ± ± controls the reflection across the x x -axis. The coefficient a a controls the amplitude. The constant d d controls the vertical shift. Here you will see that the coefficient b b controls the horizontal stretch.