Math Algebra Algebra questions and answers Name: Unit 4: Solving Quadratic Equations Date: _Bell: Homework 4: Pure Imaginary Numbers ** This is a 2-page document ** Directions: Simplify the expressions below. 1 -25 2. V 324 3. V-15 5. V-252 6. -288 7. √ 8 √24 8. 16. ſ-12-√5 11 11. 15:41 12. 8i.-91-6 13 (-41)3 2i 14. (21) (16)
Unit 4 Quadratics Test Review.pdf – 7 Date: 3/1/21 Name: Pd: Advanced Algebra with Trig REVIEW Summative U2.S1-S5 Quadratic Functions For #1-6 | Course Hero
In the standard form of quadratic equations, there are three parts to it: ax^2 + bx + c where a is the coefficient of the quadratic term, b is the coefficient of the linear term, and c is the constant. The –4 at the end of the equation is the constant. This hopefully answers your last question. Now, your first question.
Source Image: studiestoday.com
Download Image
Algebra (all content) 20 units · 412 skills. Unit 1 Introduction to algebra. Unit 2 Solving basic equations & inequalities (one variable, linear) Unit 3 Linear equations, functions, & graphs. Unit 4 Sequences. Unit 5 System of equations. Unit 6 Two-variable inequalities. Unit 7 Functions. Unit 8 Absolute value equations, functions, & inequalities.

Source Image: yumpu.com
Download Image
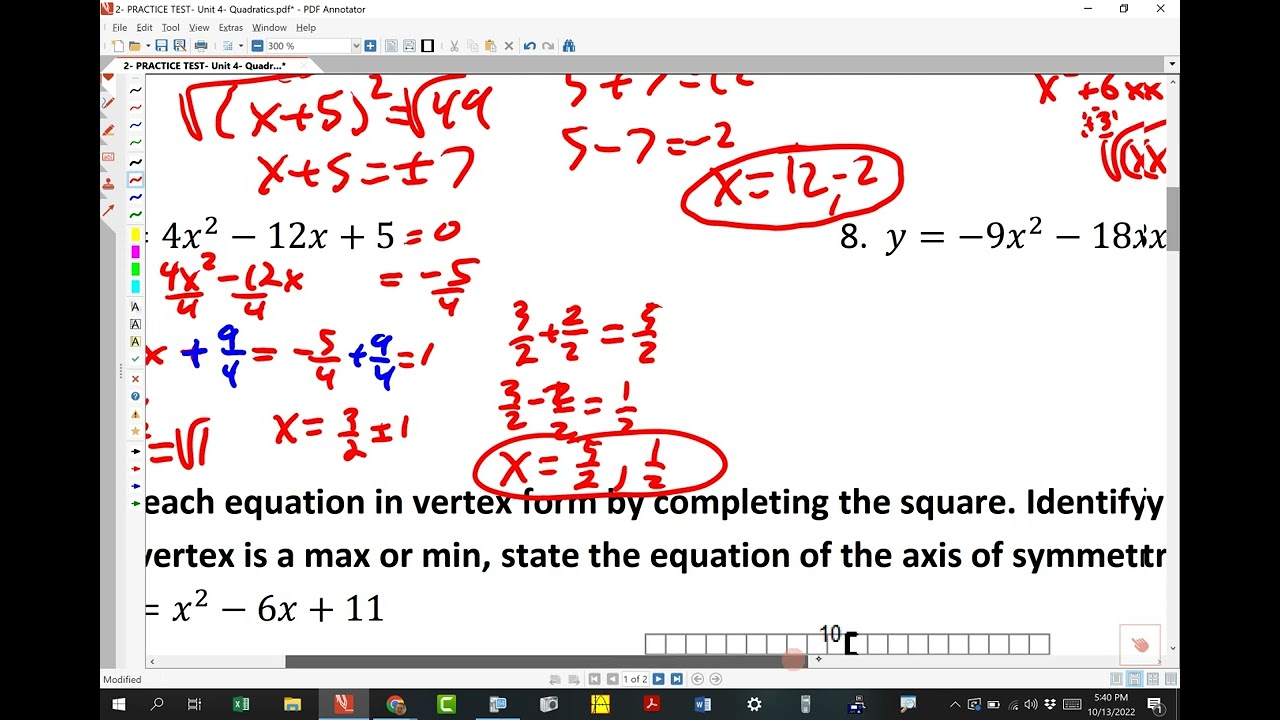
Practice Test Unit 4 Quadratics – YouTube Jun 4, 2023Solve the following quadratic equations. (We will show the check for problem 1.) Example 10.3.1. x2 − 7x + 12 = 0 The equation is already set equal to 0 (x − 3)(x − 4) = 0 Factor. Set each factor equal to 0. x − 3 = 0 or x − 4 = 0 x = 3 or x = 4. Check: If x = 3, x2 − 7x + 12 = 0.
![Name: _Algebra 2 Date:_ Per: _ Unit 4: Solving Quadratic Equations Quiz 4-1: Graphing, Fac [algebra]](https://p16-ehi-va.gauthmath.com/tos-maliva-i-ejcjvp0zxf-us/61b273919d1e4ca7b88c7bae3f8f9027~tplv-ejcjvp0zxf-webp.webp)
Source Image: gauthmath.com
Download Image
Unit 4 Solving Quadratic Equations Answer Key
Jun 4, 2023Solve the following quadratic equations. (We will show the check for problem 1.) Example 10.3.1. x2 − 7x + 12 = 0 The equation is already set equal to 0 (x − 3)(x − 4) = 0 Factor. Set each factor equal to 0. x − 3 = 0 or x − 4 = 0 x = 3 or x = 4. Check: If x = 3, x2 − 7x + 12 = 0. 9.2 Solve Quadratic Equations by Completing the Square; 9.3 Solve Quadratic Equations Using the Quadratic Formula; 9.4 Solve Quadratic Equations in Quadratic Form; 9.5 Solve Applications of Quadratic Equations; 9.6 Graph Quadratic Functions Using Properties; 9.7 Graph Quadratic Functions Using Transformations; 9.8 Solve Quadratic Inequalities
Name: _Algebra 2 Date:_ Per: _ Unit 4: Solving Quadratic Equations Quiz 4-1: Graphing, Fac [algebra]
show steps by steps Show transcribed image text There are 2 steps to solve this one. Expert-verified Step 1 Given quadratic equation: f ( x) = − x 2 + 15 x − 56 To Find: Solution. Calculations:- Analytically solving:- Equating f ( x) = 0 View the full answer Step 2 Unlock Answer Unlock Previous question Next question Transcribed image text: NCERT Solutions for Class 11 Maths Chapter 5 – Complex Numbers and Quadratic Equations – MathonGo

Source Image: mathongo.com
Download Image
4.9 – Homework Guide show steps by steps Show transcribed image text There are 2 steps to solve this one. Expert-verified Step 1 Given quadratic equation: f ( x) = − x 2 + 15 x − 56 To Find: Solution. Calculations:- Analytically solving:- Equating f ( x) = 0 View the full answer Step 2 Unlock Answer Unlock Previous question Next question Transcribed image text:
Source Image: coachself.weebly.com
Download Image
Unit 4 Quadratics Test Review.pdf – 7 Date: 3/1/21 Name: Pd: Advanced Algebra with Trig REVIEW Summative U2.S1-S5 Quadratic Functions For #1-6 | Course Hero Math Algebra Algebra questions and answers Name: Unit 4: Solving Quadratic Equations Date: _Bell: Homework 4: Pure Imaginary Numbers ** This is a 2-page document ** Directions: Simplify the expressions below. 1 -25 2. V 324 3. V-15 5. V-252 6. -288 7. √ 8 √24 8. 16. ſ-12-√5 11 11. 15:41 12. 8i.-91-6 13 (-41)3 2i 14. (21) (16)

Source Image: coursehero.com
Download Image
Practice Test Unit 4 Quadratics – YouTube Algebra (all content) 20 units · 412 skills. Unit 1 Introduction to algebra. Unit 2 Solving basic equations & inequalities (one variable, linear) Unit 3 Linear equations, functions, & graphs. Unit 4 Sequences. Unit 5 System of equations. Unit 6 Two-variable inequalities. Unit 7 Functions. Unit 8 Absolute value equations, functions, & inequalities.
Source Image: youtube.com
Download Image
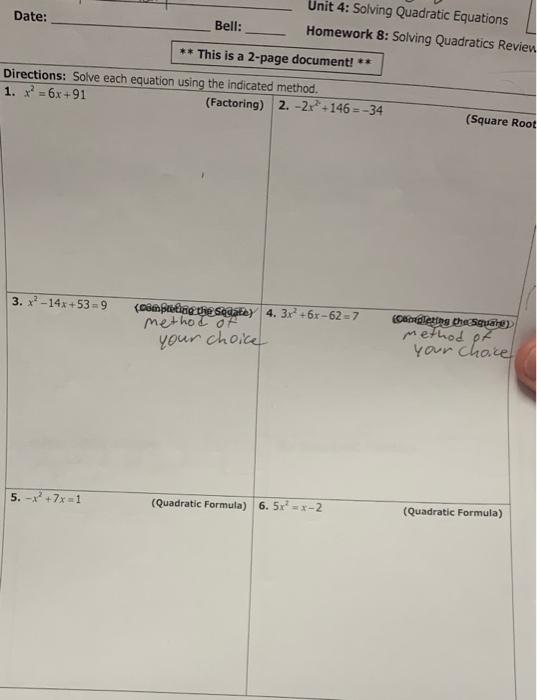
Solved Date: Bell: Unit 4: Solving Quadratic Equations | Chegg.com There are 3 steps to solve this one. Expert-verified Step 1 Given an algebraic expression: x 2 = 6 x + 91 This expression can be rewritten as : x 2 − 6 x − 91 = 0 (1) This is a quadratic equation. T… View the full answer Step 2 Unlock Step 3 Unlock Answer Unlock Previous question Next question Transcribed image text:
Source Image: chegg.com
Download Image
Quadratics (Quadratic Equations) – Definition, Formula, How to Solve Quadratics Jun 4, 2023Solve the following quadratic equations. (We will show the check for problem 1.) Example 10.3.1. x2 − 7x + 12 = 0 The equation is already set equal to 0 (x − 3)(x − 4) = 0 Factor. Set each factor equal to 0. x − 3 = 0 or x − 4 = 0 x = 3 or x = 4. Check: If x = 3, x2 − 7x + 12 = 0.

Source Image: byjus.com
Download Image
NCERT Solutions for Class 10 Maths CBSE Chapter 4: Quadratic Equations | TopperLearning 9.2 Solve Quadratic Equations by Completing the Square; 9.3 Solve Quadratic Equations Using the Quadratic Formula; 9.4 Solve Quadratic Equations in Quadratic Form; 9.5 Solve Applications of Quadratic Equations; 9.6 Graph Quadratic Functions Using Properties; 9.7 Graph Quadratic Functions Using Transformations; 9.8 Solve Quadratic Inequalities
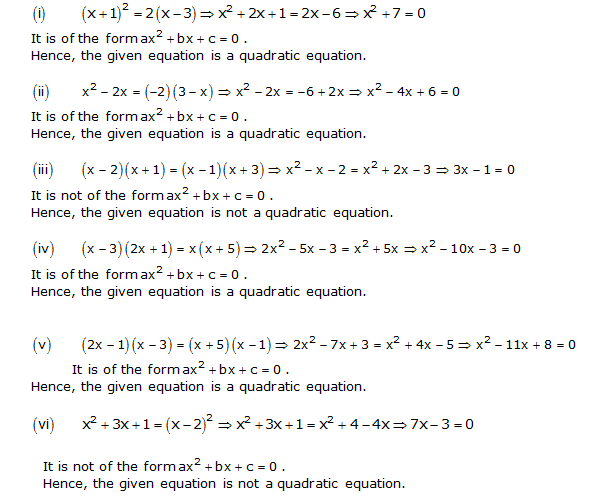
Source Image: topperlearning.com
Download Image
4.9 – Homework Guide
NCERT Solutions for Class 10 Maths CBSE Chapter 4: Quadratic Equations | TopperLearning In the standard form of quadratic equations, there are three parts to it: ax^2 + bx + c where a is the coefficient of the quadratic term, b is the coefficient of the linear term, and c is the constant. The –4 at the end of the equation is the constant. This hopefully answers your last question. Now, your first question.
Practice Test Unit 4 Quadratics – YouTube Quadratics (Quadratic Equations) – Definition, Formula, How to Solve Quadratics There are 3 steps to solve this one. Expert-verified Step 1 Given an algebraic expression: x 2 = 6 x + 91 This expression can be rewritten as : x 2 − 6 x − 91 = 0 (1) This is a quadratic equation. T… View the full answer Step 2 Unlock Step 3 Unlock Answer Unlock Previous question Next question Transcribed image text: